Lightning:

An electric discharge between cloud and earth, between clouds or between the charge centres of the same cloud is known as lightning.

Lightning is a huge spark and takes place when clouds are charged to such a high potential (+ ve or – ve) with respect to earth or a neighbouring cloud that the dielectric strength of neighbouring medium (air) is destroyed. There are several theories which exist to explain how the cloud to be charge. The most accepted one is that during the uprush of warm moist air from earth between the air and the tiny particles of water causes the building up of charges. When drops of water are formed, the larger drops become positively charged and the smaller drops become negatively charged.

When the drops of water accumulate, they form clouds, and hence cloud may possess either a positive or a negative charge, depending upon the charge of drops of water they contain. The charge on a cloud may become so great that it may discharge to another cloud or to earth and we call this discharge as lightning.

The thunder which accompanies lightning is due to the fact that lightning suddenly heats up the air, thereby causing it to expand. The surrounding air pushes the expanded air back and forth causing the wave motion of air which we recognise as thunder.

Mechanism of Lightning Discharge:

Let us now discuss the manner in which a lightning discharge occurs. When a charged cloud passes over the earth, it induces equal and opposite charge on the earth below. Fig. 24.4 shows a negatively charged cloud inducing a positive charge on the earth below it. As the charge acquired by the cloud increases, the potential between cloud and earth increases and, therefore, gradient in the air increases. When the potential gradient is sufficient (5 kV/cm to 10 kV/cm) to break down the surrounding air, the lightning stroke starts. The stroke mechanism is as under :

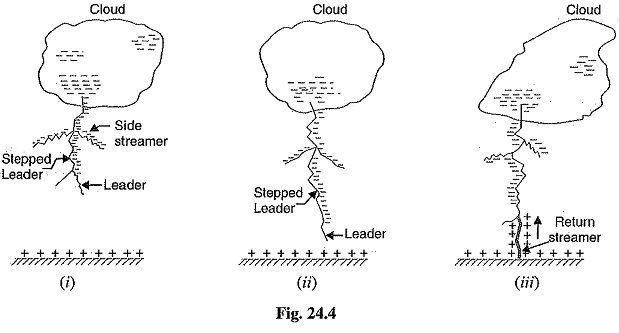(i) As soon as the air near the cloud breaks down, a streamer called leader streamer or pilot streamer starts from the cloud towards the earth and carries charge with it as shown in Fig. 24.4 (i). The leader streamer will continue its journey towards earth as long as the cloud, from which it originates feeds enough charge to it to maintain gradient at the tip of leader streamer above the strength of air. If this gradient is not maintained, the leader streamer stops and the charge is dissipated without the formation of a complete stroke.

In other words, the leader streamer will not reach the earth. Fig. 24.4 (i) shows the leader streamer being unable to reach the earth as gradient at its end cloud not be maintained above the strength of air. It may be noted that current in the leader streamer is low (<100 A) and its velocity of propagation is about 0.05% that of velocity of light. Moreover, the luminosity of leader is also very low.

(ii) The path of leader streamer is a path of ionisation and, therefore, of complete breakdown of insulation. As the leader streamer reaches near the earth, a return streamer shoots up from the earth [See Fig. 24.4 (iii)] to the cloud, following the same path as the main channel of the downward leader.

The action can be compared with the closing of a switch between the positive and negative terminals; the downward leader having negative charge and return streamer the positive charge. This phenomenon causes a sudden spark which we call lightning. With the resulting neutralization of much of the negative charge on the cloud, any further discharge from the cloud may have to originate from some other portion of it.

The following points may be noted about lightning discharge :

• A lightning discharge which usually appears to the eye as a single flash is in reality made up of a number of separate strokes that travel down the same path. The interval between them varies from 0.0005 to 0.5 second. Each separate stroke starts as a downward leader from the cloud.
• If has been found that 87% of all lightning strokes result from negatively charged clouds and only 13% originate from positively charged clouds,
• It has been estimated that throughout the world, there occur about 100 lightning strokes per
• Lightning discharge may have currents in the range of 10 kA to 90 kA.