Higher Order Filter Design:
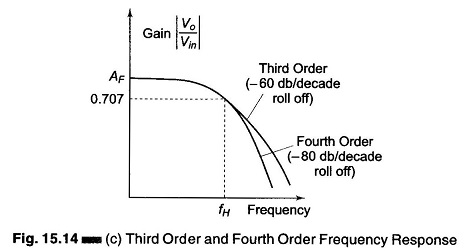
Higher Order Filter Design – From the preceding discussion on filters we can conclude that in the stop band the gain of the filter changes at the rate of 20 db/decade for first order filters and 40 db/decade for second order filters. This means that as the order of the filter is increased, the actual stop band response of the filter approaches its ideal stop band characteristics.
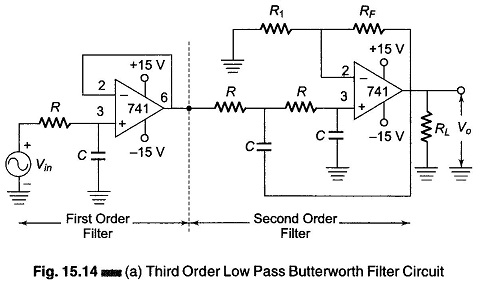
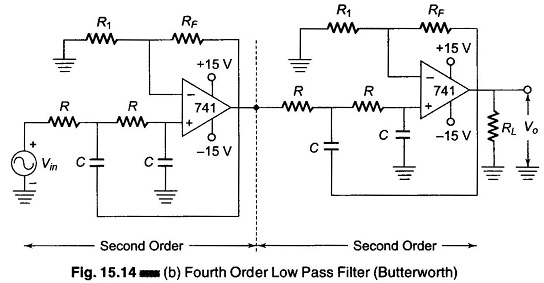
Higher order filter design, such as third, fourth, fifth and so on are formed simply by using first and second order filters. For example, a third order low pass filter is formed by cascading or connecting first and second order low pass filters in series. A fourth order low pass filter is composed of two cascaded second order low pass filter sections. There is no limit to the order of the filter that can be formed; as the order of the filter increases, so does its size. Also, the accuracy declines, in that the difference between the actual stop band response and the ideal stop band response increases with an increase in the order of the filter.
Figure 15.14, shows third and fourth order low pass Butterworth filters. In a third order filter the voltage gain of the first order section is one and that of the second order section is two.
In a fourth order filter the gain of the first section is 1.152 while that of the second section is 2.235. These gain values are necessary to guarantee Butterworth response and must remain the same regardless of the filter cutoff frequency. Also, the overall filter gain is equal to the product of the individual voltage gains of the filter sections. Hence, the overall gain of a third order filter is 2.0 and that of the fourth order is (1.152) x (2.235) = 2.57.
Since the frequency determining resistors and capacitors are equal, the high cutoff frequencies of the third and fourth order low pass filters in Figs 15.14 (a) and (b) must also be equal, and are given by
As with first and second order filters, third and fourth order high pass filters are formed by simply interchanging the position of frequency determining resistors and capacitors. The overall gain of higher order filter design is fixed because all the frequency determining resistors and capacitors are equal.