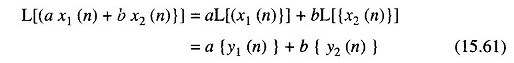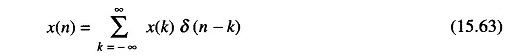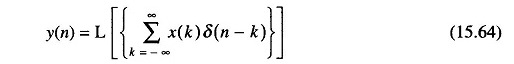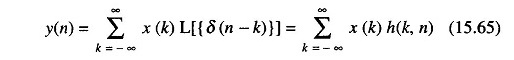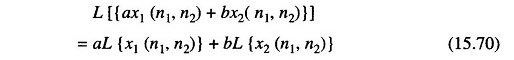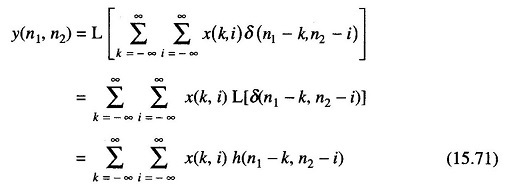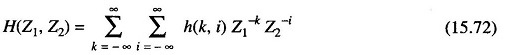What is Digital System?:

Fundamental Properties of 1-D Digital System : A digital system can be defined as an operator which transforms an input sequence { x(n)} to an output sequence {y(n)}

A system of this type is said to be linear, indicated by the symbol L, if and only if the principle of superposition holds. This is equivalent to saying that if {y₁(n)} and {y₂(n)} are the outputs of the system with inputs {x₁(n)} and {x₂(n)}, then

where a and b are arbitrary constant.

Since linearity is valid (for absolutely convergent systems) for the sum of an infinite number of terms, the linear system can be uniquely determined by its response to a unit sample sequence defined as the sequence.

We can obtain another input-output relation as follows. By observing that the generic sample x(n) of the input signal can be written in the form

The input-output relation can be written as

and from linearity properties

where { h (k, n)} is the response to the unit sample sequence, which in general is a function of k and n.

A more useful relation is obtainable for a subclass of linear systems, the shift-invariant linear system. These systems are characterized by the property that if {y(n)} is the response to {x(n)} then {y(n – k)} is the response to {x(n – k)}.

In this case the response of the system to the impulse { (n – k) } is { h(n – k)) and the input-output relation can be written as:

This relation, which is commonly written in the symbolic form

is called the convolution sum of {x(n)} and {h(n)}. The sequence {h(n)} is called the impulse response of the system.

In Z-transform domain, the convolution equation reduces to the form

where

is the Z-transform of the unit-impulse response. H(Z) is called the Z-transform function of the system and characterizes completely the linear shift invariant system.

Fundamental Properties of 2-D Digital System : The same definitions as previously can be given in the 2-D case. A 2-D system can be characterized by an operator transforming an input 2-D sequence {x(n₁, n₂)} to an output 2-D sequence { y(n₁, n₂)}. The system is linear if and only if the principle of superposition holds if

If {h(n₁ – k, n₂ – i)} is the output of the system to the unit pulse {δ(n₁ – k, n₂ – i)}, the convolution sum can be obtained by writing the output signal in the form

In the 2-D Z-domain the convolution operator reduces to a multiplication

where the function

is called the Z-transfer function of the system. Obviously this function is the 2-D Z-transform of the impulse response h(k, i).