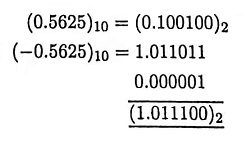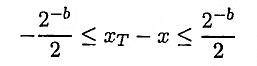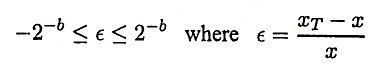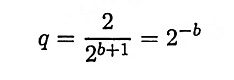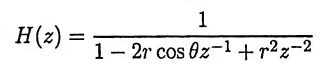Finite Word Length Effects in Digital Filters Interview Questions and Answers:
1. What are the different types of arithmetic in digital systems?
Ans. There are three types of arithmetic used in digital systems
- Fixed point arithmetic
- Floating point arithmetic
- Block Floating arithmetic.
2. What do you understand by a fixed-point number?
Ans. In fixed-point arithmetic the position of the binary point is fixed. The bit to the right represent the fractional part of the number and those to the left represent the integer part. For example, the binary number 01.1100 has the value 1.75 in decimal.
3. What are the different types in fixed-point number representation?
Ans. Depending on the way negative numbers are represented, there are three different forms of fixed-point arithmetic. They are 1) sign-magnitude 2) l’s complement 3) 2’s complement
4. What do you understand by sign-magnitude representation?
Ans. For sign-magnitude representation the leading binary digit is used to represent the sign. If it is equal to 1 the number is negative, otherwise the number is positive. For example, the decimal number -1.75 is represented as 11.110000 and 1.75 is represented as 01.110000. In sign-magnitude form the number 0 has two representations, i.e., 00.000000 or 10.000000. With b bits only 2b – 1 numbers can be represented.
5. Write a short note on l’s complement representation?
Ans. In one’s complement form the positive number is represented as in the sign-magnitude system. To obtain the negative of a positive number, one simply complements all the bits of the positive number. For example, the negative of 01.110000 would be represented as -(01.110000)2 = (10.001111)2
6. What do you understand by 2’s complement representation?
Ans. In two’s complement representation positive numbers are represented as in sign magnitude and one’s complement. The negative number is obtained by complementing all the bits of the positive number and adding one to the least significant bit. For example
7. Write an account on floating point arithmetic.
Ans. In floating point representation a positive number is represented as F = 2C.M where M, called mantissa, is a function such that 1/2 ≤ M < 1 and C, the exponent can be either positive or negative.
The decimal number 2.25, 0.75 have floating point representations as
2.25 = 22 x 0.5625 = 2010 x 0.1001
and
0.75 = 20 x 0.75 = 2000 x 0.1100 respectively
Negative floating point numbers are generally represented by considering the mantissa as a fixed point number. The sign of the floating point number is obtained from the first bit of mantissa.
8. What is meant by block floating point representation? What are its advantages?
Ans. In block floating point arithmetic the set of signals to be handled is divided into blocks. Each block have the same value for the exponent. The arithmetic operations with in the block uses fixed point arithmetic and only one exponent per block is stored thus saving memory. This representation of numbers is most suitable in certain FFT flow graphs and in digital audio applications.
9. What are the advantages of floating point arithmetic?
Ans.
- Larger dynamic range.
- Overflow in floating point representation is unlikely.
10. Compare the fixed point and floating point arithmetic
Ans.
| Fixed Point Arithmetic | Floating Point Arithmetic | |
| 1 | Fast operation | Slow operation |
| 2 | Relatively economical. | More expensive because of costlier hardware. |
| 3 | Small dynamic range | Increased dynamic range. |
| 4 | Roundoff error occur only for addition |
Roundoff errors can occur with both addition and multiplication. |
| 5 | Overflow occur in addition. | Overflow does not arise. |
| 6 | Used is small computers. | Used in larger, general purpose computes. |
11. What are the three quantization errors due to finite word length registers in digital filters?
Ans.
- Input quantization error.
- Coefficient quantization error.
- Product quantization error.
12. Brief on coefficient inaccuracy. (or) What is coefficient quantization error? What is it’s effect?
Ans. The filter coefficient are computed to infinite precision in theory. But, in digital computation the filter coefficients are represented in binary and are stored in registers.
If a b bit register is used, the filter coefficients must be rounded or truncated to b bits, which produces an error.
Due to quantization of coefficients, the frequency response of the filter may differ appreciably from the desired response and some times the filter may actually fail to meet the desired specifications. If the poles of desired filter are close to the unit circle, then those of the filter with quantized coefficients may lie just outside the unit circle, leading to unstability.
13. What is product quantization error (or) What is product roundoff error in digital signal processing?
Ans. Product quantization errors arise at the output of a multiplier. Multiplication of a b bit data with a b bit coefficient results a product having 2b bits. Since a b bit register is used, the multiplier output must be rounded or truncated to b bits, which produces an error. This error is known as product quantization error.
14. What do you understand by input quantization error?
Ans. In digital signal processing, the continuous time input signals are converted into digital using a b-bit ADC. The representation of continuous signal amplitude by a fixed digit produce an error, which is known as input quantization error.
15. What are the different quantization methods?
Ans. The common methods of quantization are
- Truncation
- Rounding
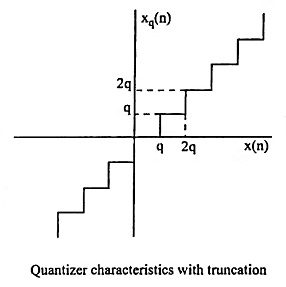
16. What is truncation?
Ans. Truncation is process of discarding all bits less significant than least significant bit that is retained.
17. What is meant by rounding? Discuss it’s effect on all types of number representations.
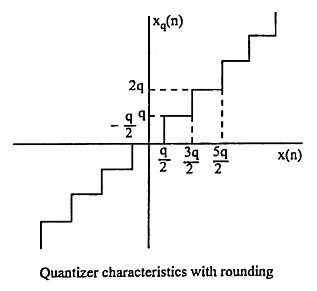
Ans. Rounding a number to b bits is accomplished by choosing the rounded result as the b bit number closest to the original number unrounded.
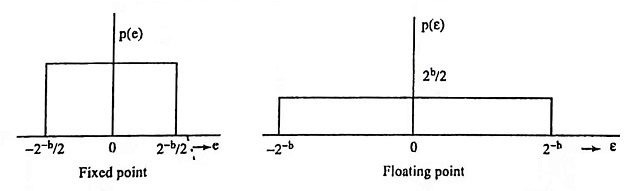
For fixed point arithmetic, the error made by rounding a number to b bits satisfies the inequality
for all three types of numbers systems, i.e, two’s-complement, one’s-complement and sign-magnitude.
For floating point numbers the error made by rounding a number to b bits satisfies the inequality
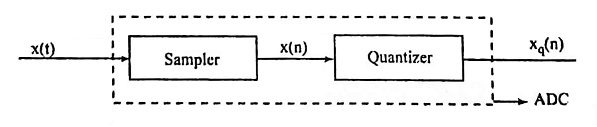
18. What is meant by A/D conversion noise?
Ans. A digital signal processor contains a device, A/D converter that operates on the analog input x(t) to produce xq(n) which is binary sequence of 0s and 1s.
At first the signal x(t) is sampled at regular intervals to produce a sequence x(n) is of infinite precision. Each sample x(n) is expressed in terms of a finite number of bits giving the sequence xq(n). The difference signal e(n) = xq(n) – x(n) is called A/D conversion noise
19. What is the effect of quantization on pole locations?
Ans. Quantization of coefficients in digital filters lead to slight changes in their value. This change in value of filter coefficients modify the pole-zero locations. Sometimes the pole locations will be changed in such a way that the system may drive into unstability.
20. What is meant by quantization step size?
Ans. Let us assume a sinusoidal signal varying between + 1 and – 1 having a dynamic range 2. If ADC used to convert the sinusoidal signal employs b + 1 bits including sign bit, the number levels available for quantizing x(n) is 2b+1. Thus the interval between successive levels.
where q is known as quantization step size.
21. Draw the following
Ans.
- Quantizer characteristic with rounding
- Quantizer characteristic with truncation
22. Draw the probability density function for rounding
Ans.
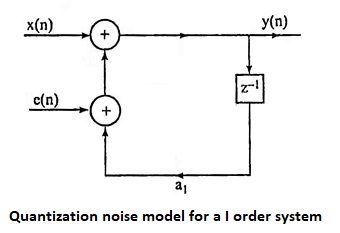
23. Draw the quantization noise model for a I order system?
Ans.
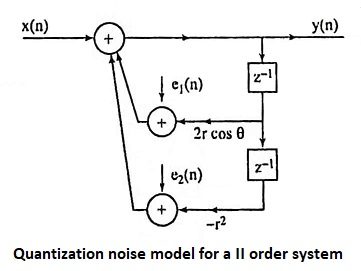
24. Draw the quantization noise model for a II order system.
Ans.
25. What is meant by (zero-input) limit cycle oscillations?
Ans. For an IIR filter, implemented with infinite precision arithmetic, the output should approach zero in the steady state if the input is zero, and it should approach a constant value if the input is a constant. However, with an implementation using finite length register an output can occur even with zero input if there is a non-zero initial condition on one of the registers. The output may be a fixed value or it may oscillate between finite positive and negative values. This effect is referred to as (zero-input) limit cycle oscillations and is due to the nonlinear nature of the arithmetic quantization.
26. What is overflow oscillations?
Ans. The addition of two fixed point arithmetic numbers cause overflow when the sum exceeds the word size available to store the sum. This overflow caused by adder make the filter output to oscillate between maximum amplitude limits. Such limit cycles have been referred to as overflow oscillations.
27. What are the methods used to prevent overflow?
Ans. There are two methods used to prevent overflow
- Saturation arithmetic,
- Scaling
28. What is meant by saturation arithmetic? What is it’s disadvantage?
Ans. When the sum of two fixed point numbers exceeds the dynamic range, overflow occurs, which causes the output of adder to oscillate between maximum amplitude limits. Such limit cycle have been referred to as overflow oscillations. One way to avoid the overflow is to modify the adder characteristics so that it performs saturation arithmetic. Thus when an overflow is sensed, the sum of the adder is set equal to the maximum value. But saturation arithmetic causes undesirable signal distortion due to non-linearity in the adder.
29. What are the two kinds of limit cycle behavior in DSP?
Ans.
- Zero input limit cycle oscillations
- Overflow limit cycle oscillations
30. Determine “dead band” of the filter.
Ans. The limit cycle occur as a result of quantization effect in multiplication. The amplitudes of the output during a limit cycle are confined to a range of values called the deadband of the filter.
31. Explain briefly the need for scaling in the digital filter implementation.
Ans. To prevent overflow, the signal level at certain points in the digital filters must be scaled so that no overflow occurs in the adder.
32. Why is the limit cycle problem does not exist when FIR digital filter is realized in direct form or cascade form?
Ans. In case of FIR filters there are no limit cycle oscillations, if the filter is realized in direct form or cascade form since these structures have no feedback.
33. Why rounding is preferred to truncation in realizing digital filter?
Ans.
- The quantization error due to rounding is independent of the type arithmetic.
- The mean of rounding error is zero.
- The variance of the rounding error signal is low.