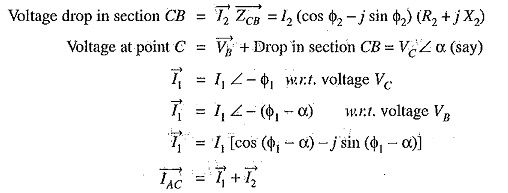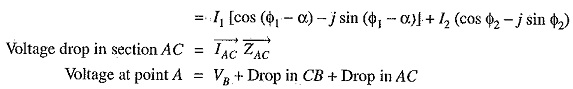AC Distribution Calculations:

AC Distribution Calculations differ from those of d.c. distribution in the following respects :

• In case of d.c. system, the voltage drop is due to resistance alone. However, in a.c. system, the voltage drops are due to the combined effects of resistance, inductance and capacitance.
• In a d.c. system, additions and subtractions of currents or voltages are done arithmetically but in case of a.c. system, these operations are done vectorially.
• In an a.c. system, power factor (p.f.) has to be taken into account. Loads tapped off form the distributor are generally at different power factors. There are two ways of referring power factor viz
• It may be referred to supply or receiving end voltage which is regarded as the reference
• It may be referred to the voltage at the load point itself.

There are several ways of solving AC Distribution Calculations. However, symbolic notation method has been found to be most convenient for this purpose. In this method, voltages, currents and imped­ances are expressed in complex notation and the calculations are made exactly as in d.c. distribution.

Methods of Solving AC Distribution Problems:

In AC Distribution Calculations, power factors of various load currents have to be considered since currents in different sections of the distributor will be the vector sum of load currents and not the arithmetic sum. The power factors of load currents may be given (i) w.r t. receiving or sending end voltage or (ii) w.r.t. to load voltage itself. Each case shall be discussed separately.

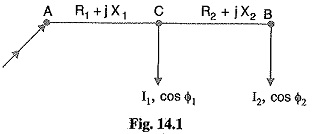
(i) Power factors referred to receiving end voltage: Consider an a.c. distributor AB with concentrated loads of I₁ and I₂ tapped off at points C and B as shown in Fig. 14.1. Taking the receiving end voltage V_B as the reference vector, let lagging power factors at C and B be cos Φ₁ and cos Φ₂ w.r.t. V_B. Let R₁,X₁ and R₂,X₂ be the resistance and reactance of sections AC and CB of the distributor.

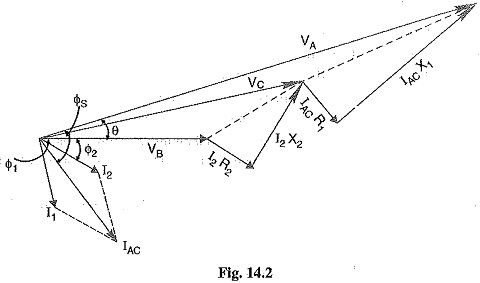
The vector diagram of the AC Distribution Calculations under these conditions is shown in Fig. 14.2. Here, the receiving end voltage V_B is taken as the reference vector. As power factors of loads are given w.r.t. V_B, therefore, I₁ and I₂ lag behind V_B by Φ₁ and Φ₂ respectively.

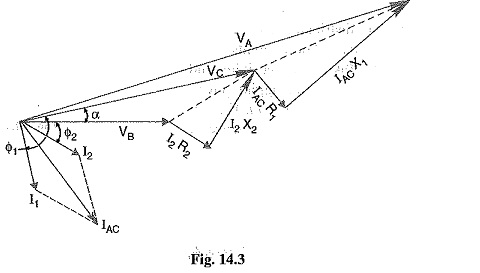
(ii) Power factors referred to respective load voltages: Suppose the power factors of loads in the previous Fig. 14.1 are referred to their respective load voltages. Then Φ₁ is the phase angle between V_C and I₁ and Φ₂ is the phase angle between V_B and I₂. The vector diagram under these conditions is shown in Fig. 14.3.