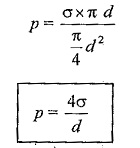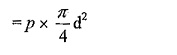Surface Tension:

Surface Tension – Due to molecular attraction, liquids have properties of cohesion and adhesion.

Cohesion is due to the force of attraction between molecules of same liquid. Otherwise, the intermolecular attraction holds the liquid molecules together is known as cohesion. This force is very small. It enables the liquid to withstand a small tensile stress. Surface tension is due to cohesion between particles at the free surface.

Adhesion is defined as the force of attraction between the molecules of two different liquids or between the molecules of the liquid and molecules of the solid boundary surface. This property enables a liquid to stick to over another body.

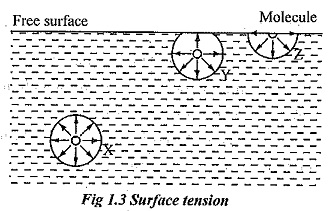
Surface tension is due to the force of cohesion between liquid particles at the free surface. A liquid molecule at the interior of the liquid are generally free to move within the liquid and they move at random, because these molecules are attracted equally in all direction by the other surrounding molecules and is in equilibrium. When they reach free surface, there are no molecules above the surface to balance the force of the molecules below it. This phenomenon is illustrated by the fig. 1.3.

Consider three molecules X, Y and Z in the liquid. Molecule X is attracted equally in all direction therefore it is in equilibrium condition. It exerts equal force in all direction. The resultant force acting on the molecule is zero. Consider molecule Y which is placed near the free surface. The upward and downward force acting on that molecule Y is unbalanced. Obviously the net resultant force is acting downward direction. The molecule Z is placed at the free surface and it has a net downward force.

However, such molecules are kept at the surface by the virtue of work done on these molecules at the time of formation of their surface. This work done on the surface against inward force is called surface energy and is generally denoted by σ (sigma). It is evident that all the molecules on the free surface exerted by a net downward force. Thus, the thin layer of molecules is formed on the free surface and it behaves as it were an elastic membrane under tension.

Surface tension is defined as the tensile force required to keep unit length of the surface film in equilibrium. It may also be defined as the force acting on the surface of the liquid when in contact with a gas surface between different immiscible liquids. The surface tension is everywhere on the surface irrespective of its curvature and acts in the the surface.

Some important real life examples are

(i) Formation of water bubbles.

(ii) Formation of rain droplets.

(iii) Collection of dust particles on water surface.

(iv) A small needle can gently placed on the liquid surface without sinking.

(v) Breakup of liquid jets.

(vi) Capillary rise and capillary siphoning.

Surface tension depends directly upon the intermolecular cohesion and hence the cohesion decreases with temperature rise, the surface tension also decreases with rise in temperature. It also depends upon the following factors.

(i) Nature of the liquid.

(ii) Nature of the surrounding liquid.

(iii)Kinetic energy of the liquid.

Surface tension in liquid droplet:

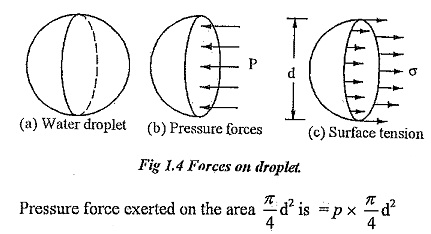
A liquid droplet is formed by surface tension. The tensile force due to surface tension is acting on the entire surface of the droplet.

Let,

P — Pressure inside the droplet above outside pressure.

σ — Surface tension of the liquid.

d — Diameter of the droplet.

Surface tension force acting around the circumference = σ x πd.

Under the equilibrium condition, these forces are equal and opposite.

From the above relation we can conclude that with an increase in size if the droplet the pressure intensity decreases.

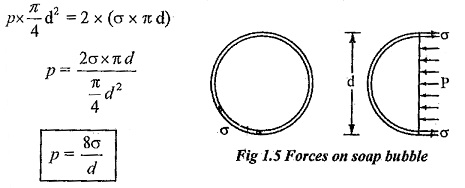
Surface tension in a soap bubble:

A soap bubble is a hollow bubble in which air has two surfaces in contact with bubble, one inside and other outside.

Pressure inside the soap bubble

Surface tension on both sides of the bubble =  2 x (σ x π d)

Equating above two equation

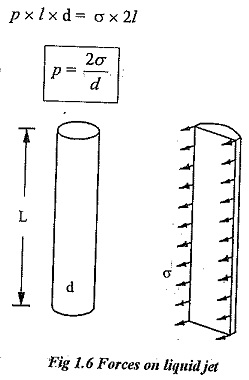
Surface tension on a liquid jet:

Consider a liquid jet of diameter ‘d’ and length ‘l’ as shown in fig.1.6.

Force due to pressure =p x l x d

Surface tension in jet = σ x 2l

Equating the above two equations