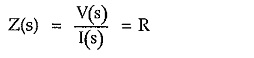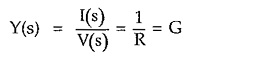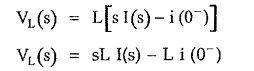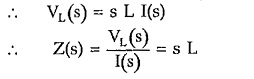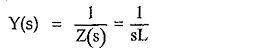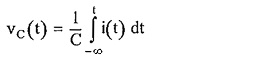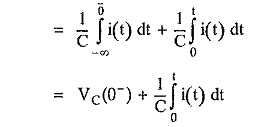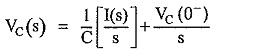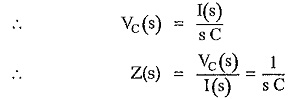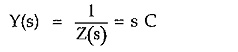s domain:

To Understand the concept of s domain network, let us see the below three points

1. Single Resistor in s Domain
2. Single Inductor in s Domain
3. Single Capacitor in s Domain

Single Resistor in s Domain:

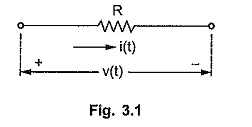
Consider a single resistor, carrying a current i(t) shown in the Fig. 3.1.

The voltage across it is v(t).

According to Ohm’s Law,

Taking Laplace transform of the equation,

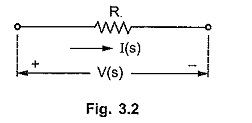
The equivalent circuit in the Laplace domain is shown in the Fig. 3.2.

The ratio of V(s) to I(s) is called transform impedance, denoted as Z(s).

So from the above equation,

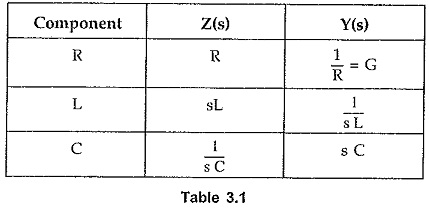
Thus transform impedance of resistance is resistance itself. Similarly the ratio of I(s) to V(s) is called transform admittance denoted as Y(s).

Thus transform admittance of resistance is conductance G.

Single Inductor in s Domain:

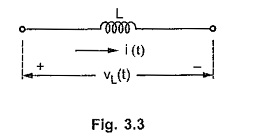
Consider a single inductor, carrying a current i(t) with voltage v_L(t) across it as shown in the Fig. 3.3.

The voltage and current in inductor are related as,

Taking Laplace transform,

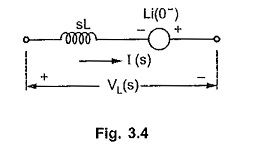
The product L i(0^–) indicates the voltage source, which takes into account the effect of initial current through inductor.

Thus the equivalent circuit becomes as shown in the Fig. 3.4, in the Laplace domain.

Let us find out the transform impedance of the inductor, assuming zero initial conditions.

Thus transform impedance of an inductor is sL in Laplace domain.

While the transform admittance is,

Single Capacitor in s Domain:

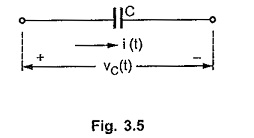
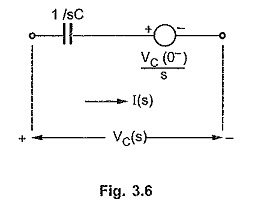
Consider a single capacitor, carrying a current i(t) with voltage v_C(t) across it. This is shown in the Fig. 3.5.

The voltage across capacitor is given by,

where V_C(0^–) indicates initial charge i.e. initial voltage on the capacitor.

To take into account the effect of initial voltage, the limits – ∞ to t are split as -∞ to 0^– and 0 to t.

Taking Laplace transform,

The initial voltage term represents voltage source V_C(0^–)/s in the Laplace domain.

Thus the equivalent circuit in the Laplace domain is shown in the Fig. 3.6.

The transform impedance of the capacitor can be obtained, by assuming zero initial voltage.

Thus the transform impedance of a capacitor is 1/s C in the Laplace domain.

While the transform admittance of the capacitor is given by,

Advantages of s domain Network:

The various advantages of s domain network are,

1. Simple to obtain by replacing each element by corresponding transform impedance, using Table 3.1.

1. All the elements behave as impedances in s domain so using various simplification techniques, the impedances can be combined easily to obtain simple form of the network.
2. The terms related to voltage drops across the elements are of simple form like [I(s) x Z(s)], according to ohm’s law.
3. No integral or differential terms are present in the set of network equations.
4. From s domain network, the system function, resultant transform impedance etc. can be obtained. These concepts are important to analyse the network in s domain.