Laplace Formula Articles:
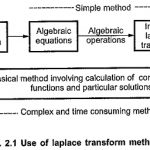
Definition of Laplace Transform: Here we are going to discuss one of such transform methods called Laplace Transform Method which transforms the time domain differential equations to the frequency domain. To understand the philosophy of transform method, let us see the … (Read More)
Laplace Transform Properties: The Laplace Transform Properties are namely, 1. Linearity: The transform of a finite sum of time functions is the sum of the Laplace transforms of the individual functions. So if F1(s), F2(s),……..Fn(s) are the Laplace transforms of the time functions f1(t), … (Read More)
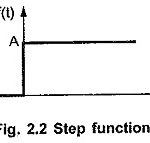
Laplace Transform of Unit Step Function: The step function is shown in the Fig. 2.2. Such a function has zero value for all t < 0, while has a value A for t ≥ 0. Hence mathematically it is expressed as, where A is … (Read More)
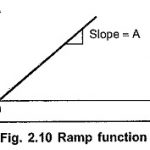
Ramp Function: The ramp function is shown in the Fig. 2.10. Mathematically such a function is expressed as, Thus it is a straight line of slope A. This slope A is called amplitude or magnitude of ramp functions. Unit Ramp Function : The ramp functions … (Read More)
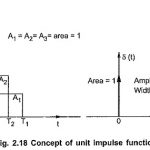
Laplace Transform of Impulse Function: The Laplace Transform of Impulse Function is a function which exists only at t = 0 and is zero, elsewhere. The impulse function is also called delta function. The unit impulse function is denoted as δ(t). … (Read More)
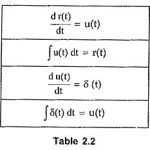
Relationships Between Standard Time Function: The Relationships between Standard Time Function contains two parts, namely Relation Between Unit Step and Unit Ramp Relation Between Unit Step and Unit Impulse 1. Relation Between Unit Step and Unit Ramp: The unit step is given by, while the unit … (Read More)
Laplace Transform of Standard Functions: The Laplace Transform of Standard Functions is given by Step Function: The unit step function is, If there is step of amplitude A i.e. f(t) = A u(t) then its Laplace is given by A/s. If the unit step is … (Read More)
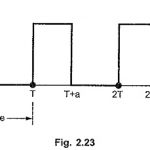
Laplace Transform of Periodic Function: Consider a Laplace Transform of Periodic Function of time period T satisfying the condition, where n is positive or negative integer. The Laplace transform of such periodic function is given by , where F1 (s) is the Laplace transform … (Read More)
Convolution Theorem: The convolution theorem of Laplace transform states that, let f1 (t) and f2 (t) are the Laplace transformable functions and F1 (s), F2 (s) are the Laplace transforms of f1 (t) and f2 (t) respectively. Then the product of … (Read More)
Inverse Laplace Transform: As mentioned earlier, inverse Laplace transform is calculated by partial fraction method rather than complex integration evaluation. Let F(s) is the Laplace transform of f(t) then the inverse Laplace transform is denoted as, The F(s), in partial fraction method, … (Read More)
Convolution Integral in Network Analysis: The Convolution Integral in Network Analysis in Laplace transform states that where f1 (t) * f2 (t) = Convolution of f1 (t) and f2 (t) From the definition of system function, Taking inverse Laplace, From the convolution theorem, where Thus with the help of convolution of … (Read More)