BCD Subtraction:

Addition of signed BCD numbers can be performed by using 9’s or 10’s complement methods. A negative BCD number can be expressed by taking the 9’s or 10’s complement. Let us see BCD Subtraction using 9’s Complement and BCD Subtraction using 10’s Complement numbers and BCD Subtraction process using it.

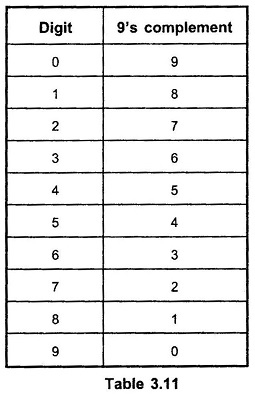
9s Complement:

The 9’s complement of a decimal number is found by subtracting each digit in the number from 9. The 9’s complement of each of the decimal digits is as follows :

BCD Subtraction using 9s Complement:

In 9s Complement subtraction when 9s Complement of smaller number is added to the larger number carry is generated. It is necessary to add this carry to the result. (this is called an end-around carry). When larger number is subtracted from smaller one, there is no carry, and the result is in 9s Complement form and negative. This is illustrated in following examples :

The 10’s complement of a decimal number is equal to the 9’s complement plus 1.

BCD Subtraction using 10s Complement:

The BCD Subtraction using 10s Complement can be used to perform subtraction by adding the minuend to the 10s Complement of the subtrahend and dropping the carry. This is illustrated in following examples.

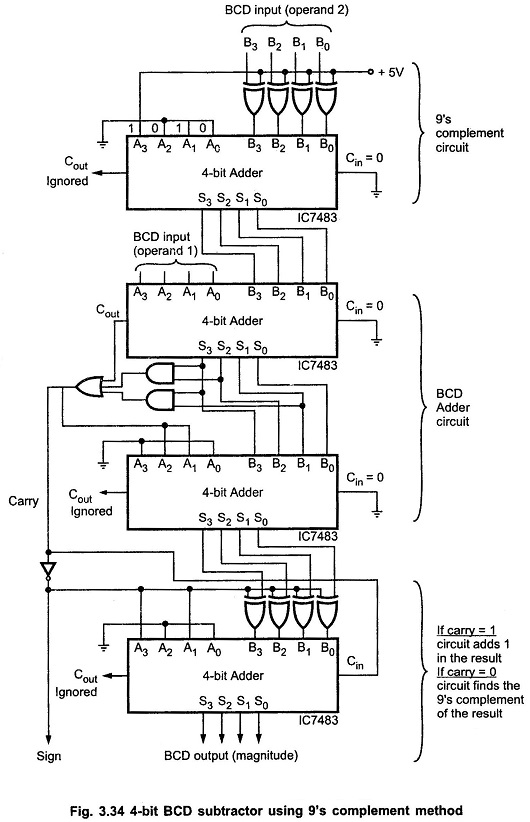
From the above examples we can summarize steps for 9s Complement BCD subtraction as follows :

• Find the 9’s complement of a negative number
• Add two numbers using BCD addition
• If carry is generated add carry to the result otherwise find the 9’s complement of the result.

Fig. 3.34 shows the logic diagram of the circuit to implement above mentioned steps to perform BCD subtraction using 9s Complement method. As shown in the Fig. 3.34, first binary adder finds the 9s Complement of the negative number. It does this by inverting each bit of BCD number and adding 10 (1 0 1 0₂) to it. Let us find the 9’s complement of 2

Next two 4-bit binary adders perform the BCD addition. The last adder finds the 9s Complement of the result if carry is not generated after BCD addition otherwise it adds carry in the result. (see Fig. 3.34)

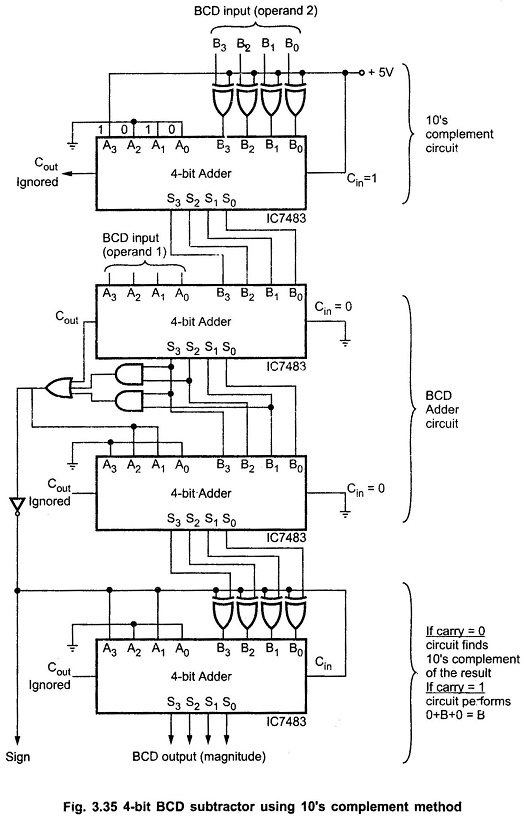
From the above examples we can summarize steps for 10s complement BCD subtraction as follows.

• Find the 10’s complement of a negative number
• Add two numbers using BCD addition
• If carry is not generated find the 10s Complement of the result.

Fig. 3.35 shows the logic diagram of the circuit to implement above mentioned steps to perform subtraction using 10s Complement method. As shown in the Fig. 3.35, first binary adder finds the 10s Complement of the negative number (9’s complement + 1). Next two 4-bit binary adders perform the BCD addition. Finally, last 4-bit binary adder finds the 10’s complement of the number if carry is not generated after BCD addition.