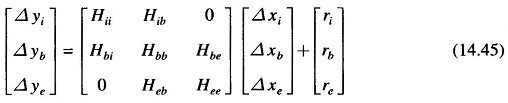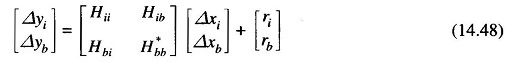External System Equivalencing in Power System:
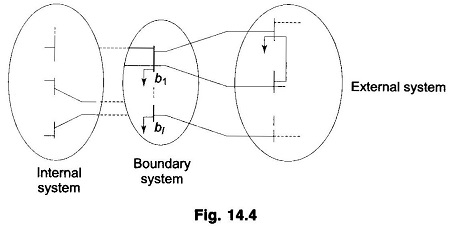
One of the widely practiced methods used for computational simplification is to divide the given system into three subsystems as shown in Fig. 14.4. One of these is referred to as the ‘internal’ subsystem and consists of those buses in which we are really interested. The second subsystem consists of those buses which are not of direct interest to us and is referred to as the ‘external’ subsystem. Finally, the buses which provide links between these internal and External System Equivalencing subsystems constitute the third subsystem referred to as the ‘boundary’ subsystem. For any given power network, the identification of the three subsystems may be done either in a natural or in an artificial way.
To illustrate the simplification of the state estimation algorithm, consider the linearized measurement equation for the injections only case. Since the system is partitioned into three subsystems, this equation may be written as
It may be noted that the internal measurement vector Δyi is not completely independent of the external subsystem state Δxe since Δyi depends on the boundary subsystem state Δxb and Δxb depends on Δxe.
where Δybe represents the injections into the boundary buses from the external buses, Δybb is the injection from the boundary buses and Δybi is the injection from the internal buses. It is assumed that the term Δybe(=HbeΔxe), may be approximated as Ĥ Δxb where Ĥ is estimated from the relation
The component Δybe may be estimated if the terms Δybi and Δybb are computed as Hbi Δxi and Hbb Δxb and then subtracted from the measured value of Δyb. This would result in part of Eq. (14.45) to be rewritten as
where H*bb = Hbb + Ĥ represents the effective Jacobian if the boundary subsystem that accounts for the effects of the external subsystem on the boundary subsystem. Equation (14.48) has a lower dimension than the original measurement equation and would therefore involve less computations. The concept of external system equivalencing may be employed with the line or mixed data situations also.