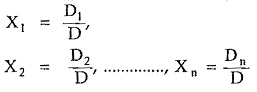Cramer Rule:
If the network is complex, the number of equations i.e. unknowns increases. In such case, the solution of simultaneous equations can be obtained by Cramer Rule for determinants.
Let us say that set of simultaneous equations obtained is, as follows :
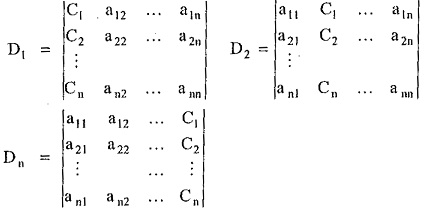
Then Cramer’s Rule says that form a system determinant Δ or D as,
Then obtain the subdeterminants Dj by replacing jth column of Δ by the column of constants existing on right hand side of equations i.e. C1,C2, … Cn;
The unknowns of the equations are given by Cramer’s Rule as,
where D1, D2,…, Dn and D are values of the respective determinants.