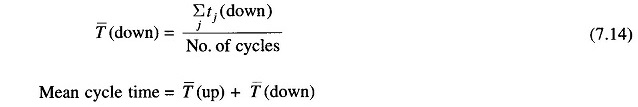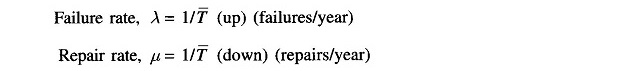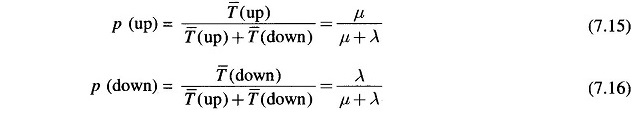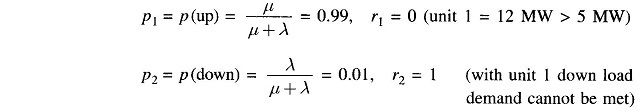Reliability Consideration in Power System:
With the increasing dependence of industry, agriculture and day-to-day household comfort upon the continuity of electric supply, the Reliability Consideration in Power System has assumed great importance. Every electric utility is normally under obligation to provide to its consumers a certain degree of continuity and quality of service (e.g. voltage and frequency in a specified range). Therefore, economy and reliability (security) must be properly coordinated in arriving at the operational unit commitment decision. In this section, we will see how the purely economic UC decision must be modified through Reliability Consideration in Power System.
In order to meet the load demand under contingency of failure (forced outage) of a generator or its derating caused by a minor defect, static reserve capacity is always provided at a generating station so that the total installed capacity exceeds the yearly peak load by a certain margin.
In arriving at the economic UC decision at any particular time, the constraint taken into account was merely the fact that the total capacity on line was at least equal to the load. The margin, if any, between the capacity of units committed and load was incidental. If under actual operation one or more of the units were to fail perchance (random outage), it may not be possible to meet the load requirements. To start a spare (standby) thermal unit and to bring it on steam to take up the load will take several hours (2-8 hours), so that the load cannot be met for intolerably long periods of time. Therefore, to meet contingencies, the capacity of units on line (running) must have a definite margin over the load requirements at all times. This margin which is known as the spinning reserve ensures continuity by meeting the load demand up to a certain extent of probable loss of generation capacity. While rules of thumb have been used, based on past experience to determine the system’s spinning reserve at any time, Patton’ s analytical approach to this problem is the most promising.
Since the probability of unit outage increases with operating time and since a unit which is to provide the spinning reserve at a particular time has to be started several hours ahead, the problem of security of supply has to be treated in totality over a period of one day. Furthermore, the loads are never known with complete certainty. Also, the spinning reserve has to be provided at suitable generating stations of the system and not necessarily at every generating station. This indeed is a complex problem. A simplified treatment of the Reliability Calculation is presented below:
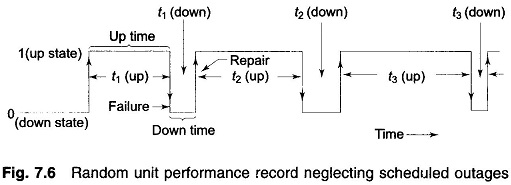
A unit during its useful life span undergoes alternate periods of operation and repair as shown in Fig. 7.6. The lengths of individual operating and repair periods are a random phenomenon with operating periods being much longer than repair periods. When a unit has been operating for a long time, the random phenomenon can be described by the following parameters.
Mean time to failure (mean ‘up’ time),
Mean time to repair (mean ‘down’ time),
Inverse of these times can be defined as rates, i.e.
Failure and repair rates are to be estimated from the past data of units (or other similar units elsewhere) by use of Eqs. (7.13) and (7.14). Sound engineering judgement must be exercised in arriving at these estimates. The failure rates are affected by preventive maintenance and the repair rates are sensitive to size, composition and skill of repair teams.
By ratio definition of probability, we can write the probability of a unit being in ‘up’ or ‘down’ states at any time as
Obviously,
p (up) and p (down) in Eqs. (7.15) and (7.16) are also termed as availability and unavailability, respectively.
When k units are operating, the system state changes because of random outages. Failure of a unit can be regarded as an event independent of the state of other units. If a particular system state i is defined as Xi units in ‘down’ state and Yi in ‘up’ state (k = Xi + Yi), the probability of the system being in this state is
Patton’s Security Function:
A breach of system security is defined as some intolerable or undesirable condition. The only breach of security considered here is insufficient generation capacity. The Patton’s security function, which quantitatively estimates the probability that the available generation capacity (sum of capacities of units committed) at a particular hour is less than the system load at that time, is defined as
where
- pi = probability of system being in state i [see Eq. (7.17)]
- ri = probability that system state i causes breach of system security.
When system load is deterministic (i.e. known with complete certainty), ri = 1 if available capacity is less than load and 0 otherwise. S indeed, is a quantitative estimate of system insecurity.
Though theoretically Eq. (7.18) must be summed over all possible system states (this in fact can be very large), from a practical point of view the sum needs to be carried out over states reflecting a relatively small number of units on forced outage, e.g. states with more than two units out may be neglected as the probability of their occurrence will be too low.
Security Constrained Optimal Unit Commitment:
Once the units to be committed at a particular load level are known from purely economic considerations, the security function S is computed as per Eq. (7.18). This figure should not exceed a certain maximum tolerable insecurity level (MTIL). MTIL for a given system is a management decision which is guided by past experience. If the value of S exceeds MTIL, the economic unit commitment schedule is modified by bringing in the next most economical unit as per the UC table. S is then recalculated and checked. The process is continued till S ≤ MTIL. As the economic UC table has some inherent spinning reserve, rarely more than one iteration is found to be necessary.
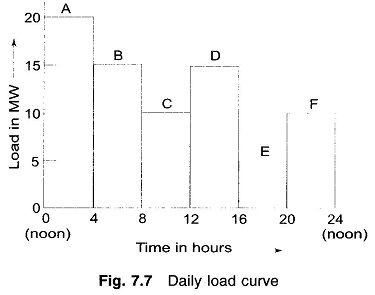
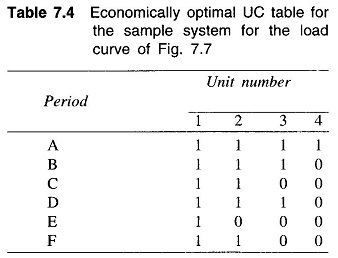
Let the daily load curve for the system be as indicated in Fig. 7.7. The economically optimal UC for this load curve is immediately obtained by use of the previously prepared UC table and is given in Table 7.4.
Let us now check if the above optimal UC table is secure in every period of the load curve.
For the minimum load of 5 MW (period E of Fig. 7.7) according to optimal UC Table 7.4., only unit 1 is to be operated. Assuming identical failure rate λ of 1/year and repair rate μ of 99/year for all the four units, let us check if the system is secure for the period E. Further assume the system MTIL to be 0.005. Unit 1 can be only in two possible states—operating or on forced outage.
Therefore,
where
Hence
Thus unit 1 alone supplying 5 MW load fails to satisfy the prescribed security criterion. In order to obtain optimal and yet secure UC, it is necessary to run the next most economical unit, i.e. unit 2 along with unit 1.
With both units 1 and 2 operating, security function is contributed only by the state when both the units are on forced outage. The states with both units operating or either one failed can meet the load demand of 5 MW and so do not contribute to the security function. Therefore,
This combination (units 1 and 2 both committed) does meet the prescribed MTIL of 0.005, i.e. S < MTIL.
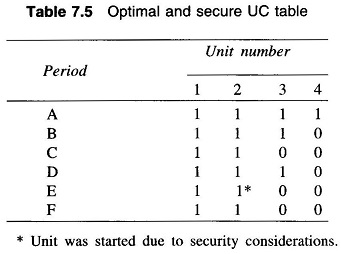
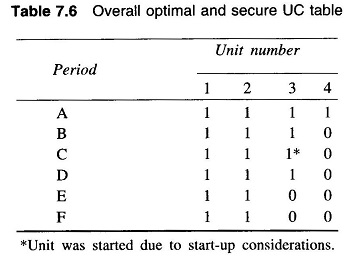
Proceeding similarly and checking security functions for periods A, B, C, D and F, we obtain the following optimal and secure UC table for the sample system for the load curve given in Fig. 7.7.
Start-up Considerations:
The UC table as obtained above is secure and economically optimal over each individual period of the load curve. Such a table may require that certain units have to be started and stopped more than once. Therefore, start-up cost must be taken into Reliability Consideration in Power System from the point of view of overall economy. For example, unit 3 has to be stopped and restarted twice during the cycle. We must, therefore, examine whether or not it will be more economical to avoid one restarting by continuing to run the unit in period C.
Case a:
When unit 3 is not operating in period C.
Total fuel cost for periods B, C and D as obtained by most economic load sharing are as under (detailed computation is avoided)
Case b:
When all three units are running in period C, i.e. unit 3 is not stopped at the end of period B.
Clearly Case b results in overall economy. Therefore, the optimal and secure UC table for this load cycle is modified as under, with due Reliability Consideration in Power System to the overall cost.