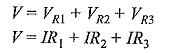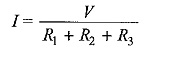KVL Law (Kirchhoff’s Voltage Law):

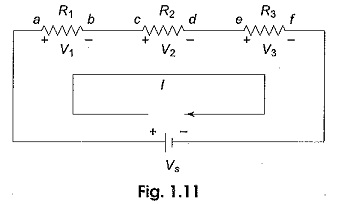
KVL Law states that the algebraic sum of all branch voltages around any closed path in a circuit is always zero at all instants of time. When the current passes through a resistor, there is a loss of energy and, therefore, a voltage drop. In any element, the current always flows from higher potential to lower potential. Consider the kirchhoff’s voltage law in Fig. 1.11. It is customary to take the direction of current I as indicated in the figure, i.e. it leaves the positive terminal of the voltage source and enters into the negative terminal.

As the current passes through the circuit, the sum of the voltage drop around the loop is equal to the total voltage in that loop. Here the polarities are attributed to the resistors to indicate that the voltages at points a, c and e are more than the voltages at b, d and f respectively as the current passes from a to f.

Kirchhoff’s Law Equation:

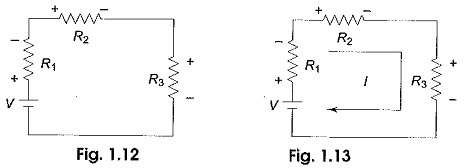
Consider the problem of finding out the current supplied by the source V in the kvl law circuit shown in Fig. 1.12.

Our first step is to assume the reference current direction and to indicate the polarities for different elements. (See Fig. 1.13).

By using Ohm’s law, we find the voltage across each resistor as follows.

where V_R1,V_R2 and V_R3 are the voltages across R_1,R₂ and R₃, respectively. Finally, by applying KVL Law, we can form the equation

From the above kirchhoff’s voltage law equation, the current delivered by the source is given by