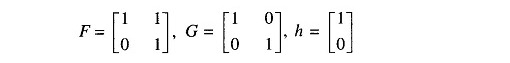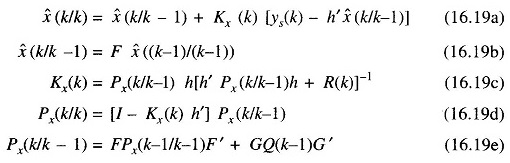Kalman Filtering Approach:

The time series approach has been widely employed in dealing with the load forecasting problem in view of the relative simplicity of the model forms. However, this method tends to ignore the statistical information about the load data which may often be available and may lead to improved load forecasts if utilized properly. In ARMA model, the model identification problem is not that simple. These difficulties may be avoided in some situations if the Kalman Filtering Approach are utilized.

Application to Short-term Forecasting

An application of the Kalman filtering algorithm to the load forecasting problem has been first suggested by Toyada et. al. for the very short-term and short-term situations. For the latter case, for example, it is possible to make use of intuitive reasonings to suggest that an acceptable model for load demand would have the form

where y_s(k) is the observed value of the stochastic load at time k, y_t(k) is the true value of this load and v(k) is the error in the observed load. In addition, the dynamics of the true load may be expressed as

where z(k) represents the increment of the load demand at time k and u₁(k) represents a disturbance term which accounts for the stochastic perturbations in y_t(k). The incremental load itself is assumed to remain constant on an average at every time point and is modelled by the equation

where the term u₂(k) represents a stochastic disturbance term.

In order to make use of the Kalman Filtering Approach, the noise terms u₁(k), u₂(k) and ν(k) are assumed to be zero mean independent white Gaussian sequences. Also, the model equations are rewritten in the form

where the vectors x(k) and u(k) are defined as

The matrices F, G and h’ are then obtained from Eqs. (16.15)-(16.17) easily and have the following values.

Based on model (16.18), it is possible to make use of the Kalman filtering algorithm to obtain the minimum variance estimate of the vector x(k) based on the data y_s(k): {y_s(1), y_s(2)…. y_s(k)}. This algorithm consists of the following equations.

where

• Q(k) = covariance of u(k)
• R(k) = covariance of ν(k)
• x̂(k/k) = filtered estimate of x(k)
• x̂(k/k-1) = single step prediction of x(k)
• K_x(k) = filter gain vector of same dimension as x(k)
• P_x(k/k) = filtering error covariance
• P_x(k/k-1) = prediction error covariance

From Eq. (16.18b) obtain the prediction x̂((k +1)/k)

From this the one step ahead load forecast is obtained as

It may be noted that filtering implies removal of disturbance or stochastic term with zero mean.

It is also possible to obtain a multi-step ahead prediction of the load from the multi-step ahead prediction of the vector x(k). For example, if the prediction x(k + d) by processing the data set Y_s(k) is required for any d > 1, it is possible to use the solution of Eq. (16.18a) for the vector x(k+ d) to get the result

In order to be able to make use of this algorithm for generating the forecast of the load y_s(k + d), it is necessary that the noise statistics and some other information be available. The value of R(k) may often be estimated from a knowledge of the accuracy of the meters employed. However, it is very unlikely that the value of the covariance Q(k) will be known to start with and will therefore have to be obtained by some means. An adaptive version of the Kalman filtering algorithm may be utilized in order to estimate the noise statistics along with the state vector x(k). Now let it be assumed that both R(k) and Q(k) are known quantities. Let it also be assumed that the initial estimate x̂(0/0) and the covariance P_x(0/0) are known. Based on these a priori information, it is possible to utilize Eq. (16.19a)-(16.19e) recursively to process the data for y_s(1), y_s(2), …y_s(k) to generate the filtered estimate x̂(k/k). Once this is available, Eq. (16.19g) may be utilized to generate the desired load forecast.