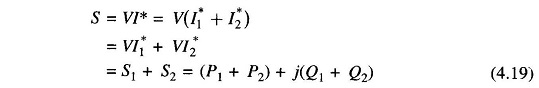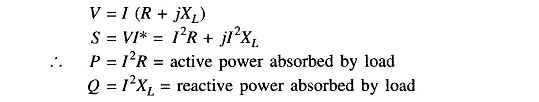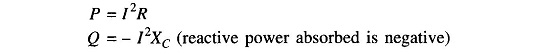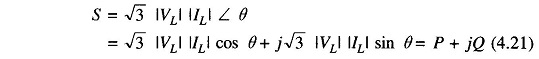Complex Power Flow in a Single Phase Load:
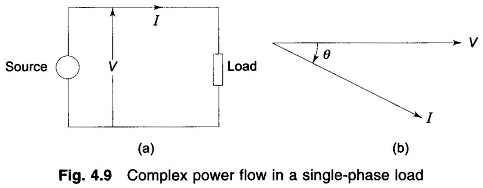
Here we are going to discuss about complex power flow in a single phase load. Consider a single phase load fed from a source as in Fig. 4.9. Let
When θ is positive, the current lags behind voltage. This is a convenient choice of sign of θ in power systems where loads have mostly lagging power factors.
Complex power flow in the direction of current indicated is given by
or
Here
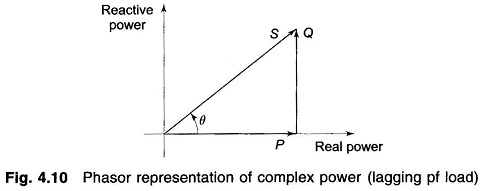
It immediately follows from Eq. (4.17) that Q, the reactive power, is positive for lagging current (lagging power factor load) and negative for leading current (leading power factor load). With the direction of current indicated in Fig. 4.9, S = P + jQ is supplied by the source and is absorbed by the load.
Equation (4.17) can be represented by the phasor diagram of Fig. 4.10 where
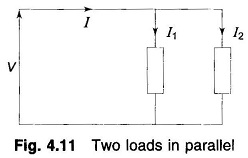
If two (or more) loads are in parallel as in Fig. 4.11
As per Eq. (4.19), Kirchhoff’s current law applies to complex power flow (also applies separately to real and reactive powers).
In a series RL load carrying current I,
In case of a series RC load carrying current I,
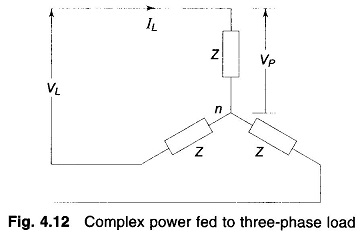
Consider now a balanced three-phase load represented in the form of an equivalent star as shown in Fig. 4.12.
The three phase complex power flow fed into load is given by
If
Then
Here
where
If VL, the line voltage, is expressed in kV; and IL, the line current in amperes, S is in kVA; and if the line current is in kiloamperes, S is in MVA.
In terms of load impedance Z,
Substituting for IL in Eq. (4.20)
If VL is in kV, S is now given in MVA. Load impedance Z if required can be calculated from