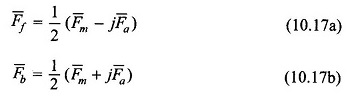Single Phase Two Winding Motor:
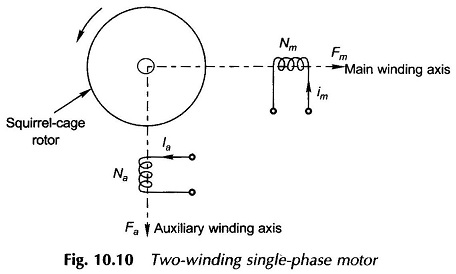
Single Phase Two Winding Motor – To understand the field phenomenon that contributes towards the generation of starting torque in a single-phase motor, it greatly helps to first study a balanced 2-phase motor. Figure 10.10 shows a 2-winding squirrel-cage motor whose stator winding axes are in relative space phase of 90° elect. The two windings are excited with currents which have a time-phase relationship of 90° elect.
where
- Im = rms value of main winding current
- Ia = rms value of auxiliary winding current
In terms of the phasor relationship
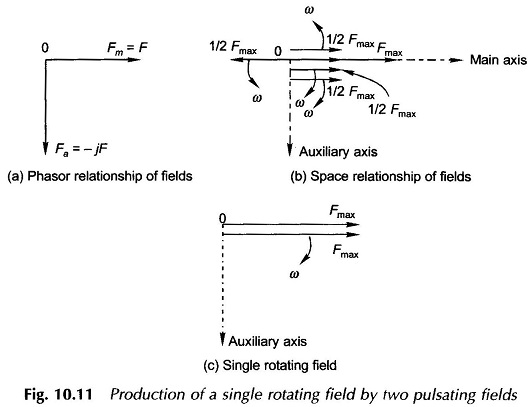
These windings therefore create two pulsating fields which are directed along their respective axes at 90° elect. to each other in space. The maximum value of peak field AT for each field is Fmax = √2 F. Figure 10.11(a) shows the time phase relationship of the pulsating main and auxiliary fields while Fig. 10.11(b) shows their space phase relationship along with their rotating components at the time instant when the main field along the winding axis has the value Fmax while the auxiliary field has zero value in accordance with the phasor diagram of Fig. 10.11(a). Of the four rotating component fields, the two rotating in counter-clockwise direction cancel out as they are in direct opposition; while the other two rotating in the clockwise direction being coincident add up to a single rotating field of magnitude Fmax as shown in Fig. 10.11(c).
From the above it is concluded that two pulsating fields, of equal strength out of time phase by 90° elect, and oriented along axes at 90° elect, in space, produce a single rotating field which rotates in the direction of leading phase to lagging phase axis.
It now easily follows that if the phase sequence of the fields is reversed, i.e. F̅m = F̅ and F̅a = jF̅ then the direction of rotation of the resultant field would also be reversed.
Unbalanced Pulsating Fields:
While the concept of a balanced 2-phase system has been used earlier, let it be redefined once again.
A set of two sinusoidal quantities constitute a balanced 2 phase system provided they have equal amplitude and a relative phase difference of 90° elect. They are known to be unbalanced otherwise.
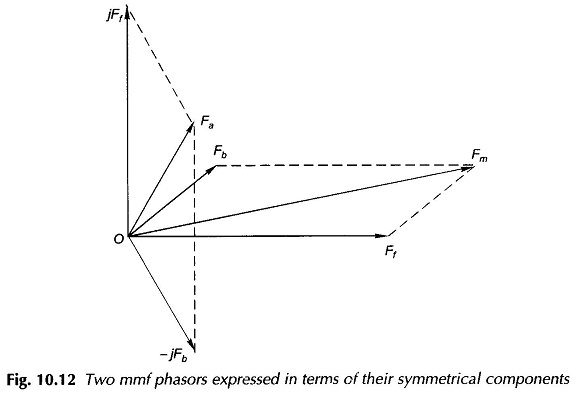
Let the pulsating fields Fm and Fa of the Two Winding Motor of Fig. 10.10 constitute an unbalanced set (this is in fact the case in a Single Phase Two Winding Motor). By the theory of 2-phase symmetrical components, the unbalanced field set can be divided into two balanced sets of opposite phase sequence. Thus,
where F̅f and jF̅f constitute one balanced (forward) set and F̅b and –jF̅b constitute the other with reversed (backward) phase sequence. The operations of Eqs. (10.16a) and (10.16b) are illustrated by the phasor diagram of Fig. 10.12.
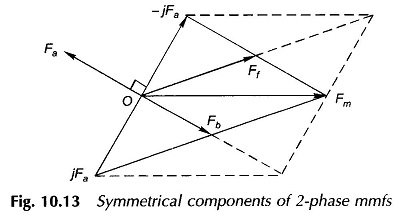
The inverse of the relationships (10.16a) and (10.16b) can be expressed as
from which the forward and backward symmetrical components can be computed for a set of two unbalanced fields. The phasor diagram depicting the operation of Eqs. (10.17a) and (10.17b) is given in Fig. 10.13.
In fact any set of phasors (may be voltages or currents) can be similarly expressed in terms of their symmetrical components and vice versa.
With reference to Eqs (10.16a) and (10.16b) it is observed that two fields Fm and Fa (assumed to be in space quadrature) can be split into two symmetrical component sets: F̅f , jF̅f and F̅b , –jF̅b . Since the component fields of each set are equal in magnitude and are in both time and space quadrature, the first set produces a forward rotating field and the second set produces a backward rotating field. It is therefore concluded that two unbalanced pulsating fields in space quadrature are equivalent to two fields rotating in opposite directions.