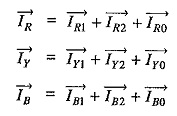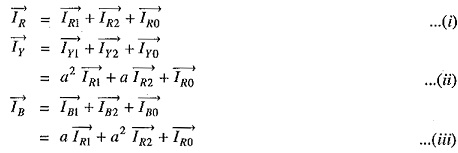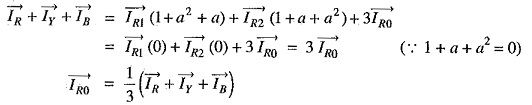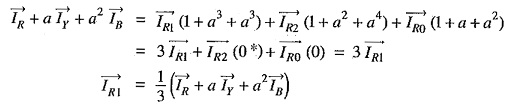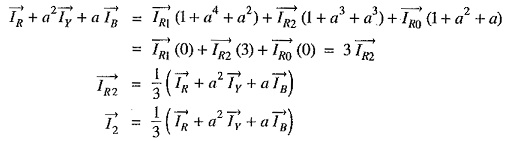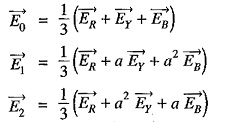Unbalanced Phase Current:

The Unbalanced Phase Current in a 3-phase system can be expressed in terms of symmetrical components as under :

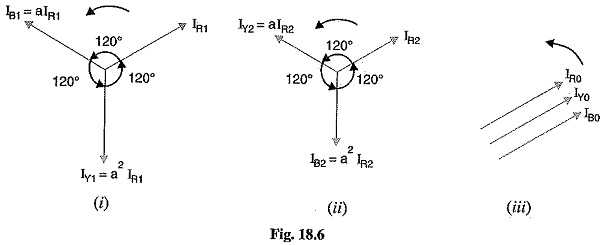
Fig. 18.6 shows the vector representation of symmetrical components. It is usually profitable in calculations to express the symmetrical components in terms of Unbalanced Phase Current. Let us express the symmetrical components of R-phase in terms of phase currents I_R,I_Y and I_B. For this purpose, express all symmetrical components of Y and B phases in terms of the symmetrical components of R-phase by means of operator ‘a’ as shown in Fig. 18.6.

Note that the positive sequence set shown in Fig. 18.6 (i) can be expressed in terms of I_R1 by means of operator a. Thus positive sequence current I_B1 in phase B leads I_R1 by 120° and, therefore, I_B1 = a I_R1 Similarly, positive sequence current in phase Y is 240° ahead of I_R1 so that I_Y1 = a² I_R1.

In an exactly similar manner, the negative sequence set can be expressed in terms of I_R2 by means of operator ‘a’ as shown in Fig. 18.6(ii). It is clear from Fig. 18.6 that :

1. Zero Sequence Current: By adding exps. (i), (ii) and (iii), we get,

As the red phase is always taken as the reference phase, therefore, subscript R is usually omitted.

2. Positive Sequence Current: Multiply exp.(ii) by ‘a’ and exp. (iii) by ‘a^2, and then adding these exps. to exp. (i), we get,

Omitting the subscript R, we have,

3. Negative Sequence Current: Multiply exp. (ii) by ‘a²‘ and exp. (iii) by ‘a’ and then adding these exps. to (i), we get,

The following points may be noted carefully :

• The currents I₁,I₂ and I₀ are the symmetrical components of R-phase. Because of the symmetry of each set, the symmetrical components of yellow and blue phases can be easily known.

• Although the treatment has been made considering currents, the method applies equally to voltages. Thus the symmetrical voltage components of R-phase in terms of phase voltages shall be :

Some Facts about Sequence Currents:

It is now desirable to get the readers acquainted with the following facts about positive, negative and zero phase sequence currents :

• A balanced 3-phase system consists of positive sequence components only; the negative and zero sequence components being zero.
• The presence of negative or zero sequence currents in a 3-phase system introduces unsymmetry and is indicative of an abnormal condition of the circuit in which these components are
• The vector sum of the positive and negative sequence currents of an Unbalanced Phase Current 3-phase system is zero. The resultant solely consists of three zero sequence currents e. Vector sum of all sequence currents in 3-phase unbalanced system

• In a 3-phase, 4 wire unbalanced system, the magnitude of zero sequence components is one-third of the current in the neutral wire i.e.

In the absence of path through the neutral of a 3-phase system, the neutral current is zero and the line currents contain no zero -sequence components. A delta-connected load provides no path to the neutral and the line currents flowing to delta-connected load can contain no zero-sequence components.

• In a 3-phase Unbalanced Phase Current system, the magnitude of negative sequence components cannot exceed that of the positive sequence components. If the negative sequence components were the greater, the phase sequence of the resultant system would be reversed,
• The current of a single phase load drawn from a 3-phase system comprises equal positive, negative and zero sequence components.