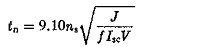Important Questions of Dynamic Electric:
1. A gear train system used to drive a load is shown in Fig. P2. Assuming the ideal conditions of no back lash and no elastic deformation in the system determine the equivalent inertia and equivalent friction referred to (a) motor shaft, (b) load shaft.
2. Show that the torque to inertia ratios referred to the motor shaft and to the load shaft differ from each other by a factor of N, where N is the gear ratio. Show that the torque squared to Inertia referred to the motor shaft or load shaft are the same.
3. Figure P2 shows a motor lifting a load by means of a winch. The weight lifted is 1500 kg at a velocity of 0.75 m/s. The motor runs at a speed of 1000 rpm. The inertia of the winch drum and motor are 1.8 kg.m2 and 3.6 kg.m2 respectively. Calculate the total load torque of the system referred to motor shaft.
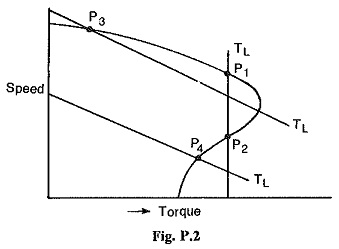
4. Use the considerations of stability to show the equilibrium of operation of the motor at points P1,P2,P3 and P4. If there is a point of instability can you suggest the modification to motor speed torque curve to make the operation stable? Based on the conclusions suggest a method to determine the speed torque curve of the motor in the first, second and fourth quadrants.
5. Use equal area of criterion to estimate the stability of a synchronous motor. Use the same to discuss the effects of damper windings on the oscillation of a synchronous motor.
6. Set up the dynamic equation of a synchronous motor during hunting and determine the expressions for natural frequency of oscillation and damped frequency of oscillation.
Determine the natural frequency of oscillation of a 50 Hz, 20 pole, 1000 kW, 6.6 kV synchronous motor having a total inertia of 2600 kg.m2 and a torque angle of 30° when the power developed is 1000 kW. If the damping power coefficient is 2.5 kW/elec. degree, determine the damped frequency of oscillation.
7. A synchronous motor connected to an infinite bus drives a mechanical load. When the motor is loaded to its rated capacity the torque angle is 45°. The load is suddenly increased to a value which corresponds to a torque angle of 60°. Determine whether the motor is stable or not. Determine also the maximum additional load that can be suddenly thrown on to the motor without affecting stability.
8. A cylindrical rotor synchronous motor having an inertia J is operating on constant voltage constant frequency busbars of voltage V. Show that its natural period of oscillation
A 10 MVA, 11 kV, 3 phase, 6 pole, 50 Hz star connected synchronous motor operates on an infinite bus. Its short circuit current is 3 times the full load current. Its natural period of oscillation is 1.4 seconds. Determine the inertia of the rotating parts.
9. A 500 kW, 10 pole, 50 Hz synchronous motor has a torque angle of 35° on full load. Determine the natural frequency of oscillation if the moment of inertia is 1200 kg.m2.
10. A 150 kW, 2300 V, 3 phase, 50 Hz, 28 pole synchronous motor is connected to constant voltage constant frequency busbars. The motor has the following data:
The moment of inertia = 460 kg.m2
Synchronising power = 12 kW/elec. degree.
Damping torque = 2500 Nm/mech/rad/sec.
Set up the electrodynamic equation of motion. Determine the natural and damped frequencies, of oscillations. If the rated load is switched on to the motor suddenly when it is on no-load determine the electromagnetic transients with and without damping torque.