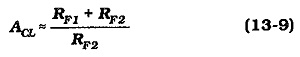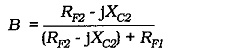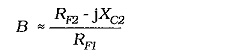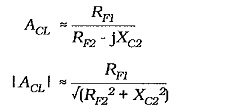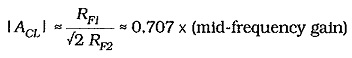Two Stage CE Amplifier using Series Voltage Negative Feedback:

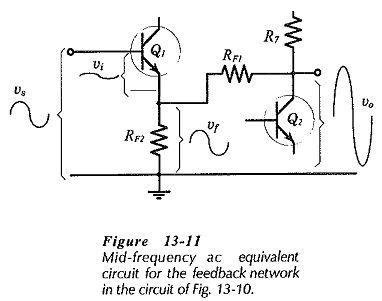
Negative Feedback Amplifier Circuit – A two-stage, capacitor-coupled BJT amplifier is shown in Fig. 13­-10. This is the same Two Stage CE Amplifier circuit discussed already with the addition of feedback components R_F2, R_F1, and C_F1. The output voltage is divided across R_F2 and R_F1 to produce a feedback voltage in series with the signal at the base of Q₁.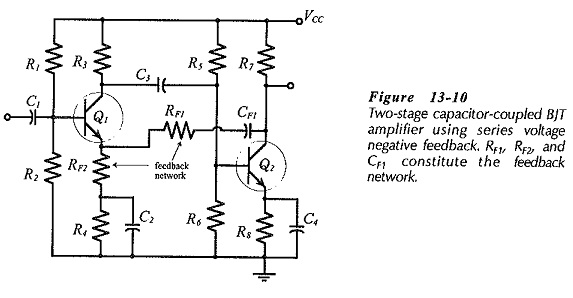 

C_F1 (in Fig. 13-10) is a dc blocking capacitor to prevent the dc voltage at Q₂ collector from affecting the Q₁ bias conditions. C_F1 behaves as an open-circuit to do and a short-circuit to ac. Consequently, C_F1 is not included in the mid-frequency no equivalent circuit of the feedback network in Fig. 13-11. Capacitor C₂ behaves as a short-circuit at middle and higher frequencies, so C₂ and R₄ (shorted by C₂) are also absent from the mid-frequency no equivalent circuit.

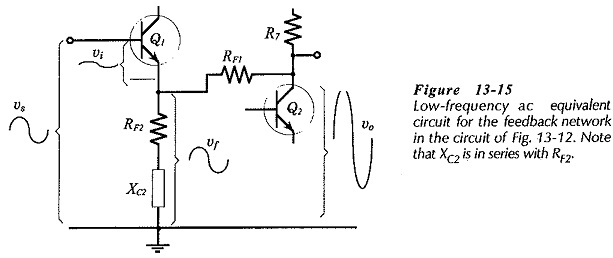
The signal voltage (v_s) is applied between Q₁ base and ground, as illustrated in Fig. 13-11, and the output voltage (v_o) is developed between Q₂ collector and ground. The feedback voltage (v_f) is developed across resistor R_F2, between the Q₁ emitter terminal and ground. The input voltage (v_i) appears across the Q₁ base-emitter terminals as the difference between v_s and v_f.

From previous topics of a Two Stage CE Amplifier, it is known that the circuit output voltage is in phase with the signal voltage. When the instantaneous level of v_s is positive-going, v_o is also positive-going, and consequently v_f is in phase-opposition with v_s. When v_s goes up (positively), v_f also goes up, and consequently, the voltage (v_i) at the base-emitter of Q₁ is reduced from v_s to,

Note that the Q₁ bias resistors (R₁ and R₂) in Fig. 13-10 are outside the feedback loop, and are unaffected by feedback. The impedance looking-into the transistor base is within the feedback loop, so it is altered by feedback. Also, recall that the Q₂ collector resistor (R₇) is unaffected by negative feedback, and that the impedance looking-into the transistor collector terminal is changed by negative feedback.

The feedback factor for the circuit in Figs. 13-10 and 13-11 is,

From Eq. 13-3,

Usually R_F1 ≫ R_F2, so

Negative Feedback Amplifier Design:

A Two Stage CE Amplifier using Series Voltage Negative Feedback amplifier like the one shown in Fig. 13-12, is best designed first as an amplifier without feedback. The feedback component values are then determined, and the circuit is modified as necessary.

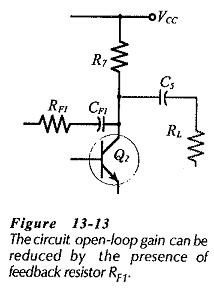
Like R_L, R_F1 is an additional load at the collector of the second stage in Fig. 13-12. As illustrated in Fig. 13-13, the voltage gain of the second stage is proportional to the total load (R_L||R₇||R_F1), consequently, R_F1 has the effect of reducing the second stage gain. A large open-loop gain is required for good gain stability, so R_F1 should be selected as large as possible.

Resistor R_F2 is an unbypassed resistor in series with the emitter of Q₁. As such, it would seem to reduce the first stage voltage gain, and thus reduce the circuit open-loop gain. However, because v_f is applied to Q₁ emitter, the effective open-loop gain is the voltage gain from the BE terminals of Q₁ to the collector of Q₂. So, R_F2 does not alter the overall open-loop gain. (R_F2 is omitted when calculating the circuit open-loop gain.)

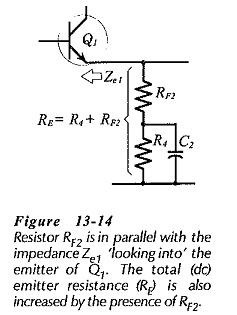
Another consideration for R_F2 is that it is in parallel with the impedance (Z_e1) at the emitter of Q₁, (see Fig. 13-14). Without negative feedback, Z_e1 would usually equal the transistor h_ib, value, which is typically 26 Ω when I_C = 1 mA. With negative feedback, Z_e1 can be shown to range from about 2.5 kΩ to 30 kΩ depending upon A_v and B. Resistor R_F2 should be selected much smaller than Z_e1. However, R_F2 should be as large as possible to give the largest possible value for R_F1; (from Eq. 13-10, R_F1 ≈ A_CL X R_F2).

A reasonable starting point for feedback network design is to select R_F2 much lower than Z_e1/10: in the range of 100 Ω to 470 Ω. R_F2 could also alter the dc bias conditions for Q₁. Consequently, it might be necessary to reduce R₄, so that R₄ and R_F2 add up to the original resistance selected for R₄ (or R_E), (see Fig. 13-14).

Figure 13-15 shows a low-frequency ac equivalent circuit for the feedback network. Note that capacitor C_F1 is still taken as an ac short circuit, so X_CF1 is assumed to be very much smaller than R_F1. The impedance of capacitor C₂ is show, and because X_C2 is assumed to be very much smaller than resistor R₄, R₄ is omitted.

From Fig. 13-15, v_o is divided across R_F1 and (R_F2 + jX_C2) to give v_f, so the feedback factor is,

Assuming that (R_F2 – jX_C2) ≪ R_F1,

From Eq. 13-3,

When X_C2 = R_F2,

To set a desired frequency lower cutoff frequency (f₁),

As already mentioned, X_CF1 must be very much smaller than R_F1 at the low cutoff frequency for the amplifier. It can be shown that, if X_CF1 = R_F1 at f₁, the closed-loop gain would actually increase at frequencies below f₁. C_F1 is normally calculated from,

Capacitor C_F1 can often be eliminated. If R_F1 is large enough, direct connection of R_F1 from Q_2C to Q_1E in Fig. 13-12 will have a negligible effect on the circuit bias conditions. In fact, with a direct-coupled circuit, direct connection of the feedback resistors might enhance the circuit bias stability.

The circuit input impedance is increased by negative feedback, so input coupling capacitor C₁ can be recalculated as a smaller capacitor, (X_C1 = Z_in/10 at f₁). Recall that the bias resistors are not affected by feedback. Regardless of how high the circuit input impedance might become, C₁ should normally be selected as a minimum of 0.1 μF, to ensure that it is much larger than any stray capacitance at the circuit input.

The emitter bypass capacitor C₄ (in Fig. 13-12) was calculated to have X_C4 = 0.65 h_ib2  at f₁. So, X_C4 will reduce the circuit open-loop gain (A_v) at f₁. However, even with this gain reduction. A_v should still be much larger than A_CL, so C₄ can normally be left as calculated for an amplifier without feedback.

Recall from earlier discussion that, when designing an amplifier without feedback, the collector resistor (R_C2) for the output transistor is usually selected as equal to, or less than, R_L/10. This is because without negative feedback Z_o ≈ R_C2. Negative feedback normally reduces Z_o to a value much smaller than R_C2. So, R_C2 does not have to be selected as R_L/10 when designing a Two Stage CE Amplifier using Series Voltage Negative Feedback. Instead, any convenient level of V_RC and I_C can be used for calculating a suitable R_C2 value.