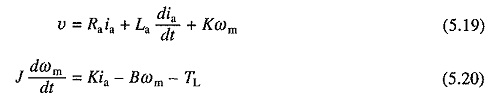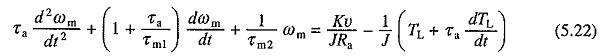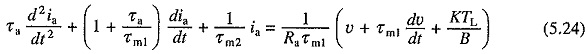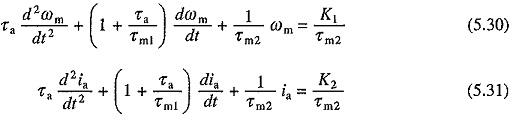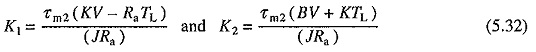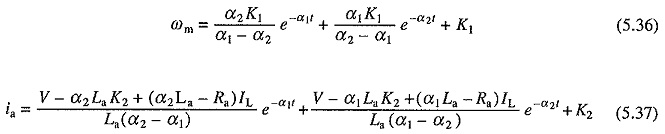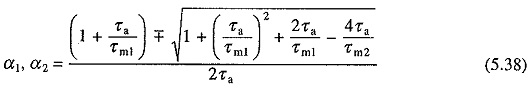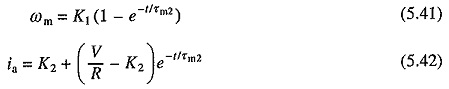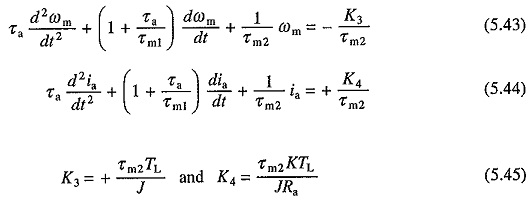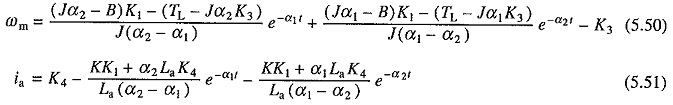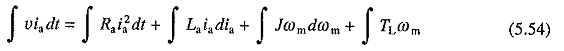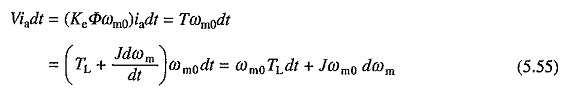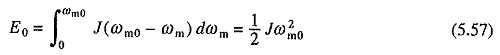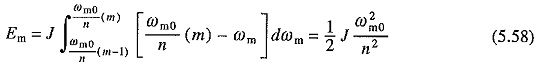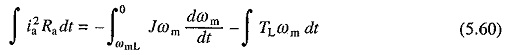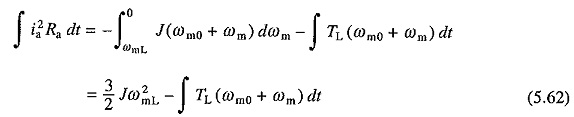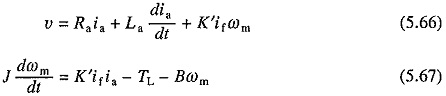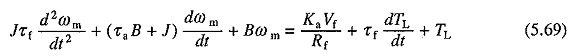Transient Analysis of DC Motor:

Starting, braking, reversing speed changing and load changing are the Transient Analysis of DC Motor which commonly occur in an industrial drive. One is interested in knowing how current, torque and speed of the driving motor change with time when under these transient operations. One is also interested in knowing energy losses, particularly those responsible for heating of the motor, and time taken for the completion of the Transient Analysis of DC Motor. This information is needed by the designer for selecting suitable rating of the motor, nature and type of its control equipment and its operation schedule, and types of protective devices and their settings.

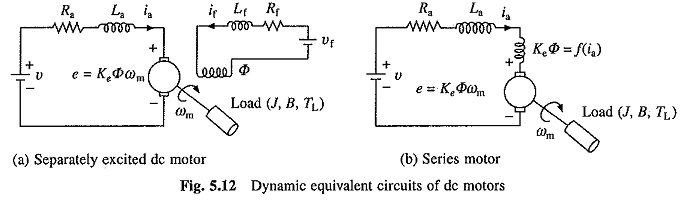
Dynamic equivalent circuits of dc motors are shown in Fig. 5.12. Source voltage v motor armature current i_a and back emf e are denoted by lower case letters to emphasize that these are instantaneous values of time varying quantities. B and J are respectively the coefficient of viscous friction in Nm/rad/sec and polar moment of inertia in kg-m² of the motor load system referred to the motor shaft.

Voltage equation of the armature circuit under transient is given by

From the dynamics of motor load system

Further

The above Transient Analysis of DC Motor are valid for any dc motor. In case of a separately excited motor when field current is maintained constant, flux remains constant, and (5.16) and (5.17) are linear differential equations. In case of a series motor, due to saturation of the magnetic circuit, flux is a nonlinear function of the armature current, and therefore, (5.16) and (5.17) are nonlinear differential equations. Even if magnetic circuit is assumed linear by neglecting saturation, (5.16) and (5.17) are nonlinear differential equations due to e being proportional to the product of i_a and ω_m, and T being proportional to i²_a. Thus, for a series motor these equations can only be solved numerically using 4th order Rungekutta method or predictor corrector method.

Transient Analysis of Separately Excited Motor with Armature Control:

When field current is kept constant, flux remains constant. Replacing K_eΦ by a constant K in Eqs. (5.16) to (5.18), yields

Differentiating Eq. (5.20) gives

Substituting in Eq. (5.19) for di_a/dt from (5.21) and rearranging terms gives

Differentiating Eq. (5.19) gives

Substituting in Eq. (5.20) for dω_m/dt from Eq. (5.23) and rearranging the terms yields

where

Equations (5.22) and (5.24) are second order linear differential equations and can be solved if the appropriate initial conditions are known. Once i_a vs t relation is obtained from Eq. (5.24), T vs t relation can be calculated.

Transient Analysis of Starting of Separately Excited Motor with Armature Control:

Transient analysis of starting process will be considered here to demonstrate how the above derived equations are utilized. It will be assumed that the motor is started with a constant voltage V impressed across its terminals against a constant load torque T_L and with a fixed resistance R_a in its armature circuit.

It is customary to assume that the motor starts only after its developed torque exceeds load torque. For this motor current should reach the value I_L given by

When motor is connected to the supply, initial value of current is zero and due to armature circuit inductance it takes some time to reach the value I_L. During whole of this period, which will be termed as first interval of the transient response, motor remains at standstill and so its back emf remains zero. Motor behaves like a simple R_a – L_a load. Hence its current is given by

Second interval of transient response starts after current reaches the value I_L. Since V and T_L are constants, dv/dt and dT_L/dt will be zero. Substituting these values in Eqs. (5.22) and (5.24) gives

where

K₁ and K₂ represent the steady state values of speed and current receptively with load torque equal to T_L.

Initial conditions needed for the solution of Eqs. (5.30) and (5.31) are

Since at the beginning of this interval, motor torque is equal to load torque, from Eq. (5.17)

Further from Eq. (5.16)

Solutions of Eqs. (5.30) and (5.31) with the initial conditions given by (5.33) to (5.35), will have the form:

where α₁ and α₂ are roots of characteristic equation and are given by

Note that the above equations have been derived by measuring time from the beginning of the second interval.

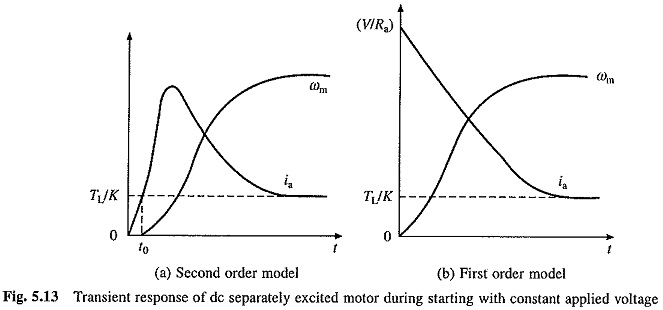
For motors less than 1000 kW, roots α₁ and α₂ are usually real. For larger and also for small and medium size motors with an external inductance connected in the armature circuit, as in the case of some chopper and rectifier fed Transient Analysis of DC Motor, roots can be complex. The nature of ω_m vs t and i_a vs t curves for starting transients, when roots are real, are shown in Fig. 5.13(a).

In small size motors, τ_a is very small due to a large armature winding resistance. It can, therefore, be neglected. Substituting τ_a = 0 in Eqs. (5.30) and (5.31) gives

Since τ_a = 0, current jumps to the value V/R_a in zero time. Thus, initial conditions are

Solutions of Eqs. (5.39) and (5.40) yield

Nature of ω_m versus t and i_a versus t curves based on these equations are shown in Fig. 5.13(6).

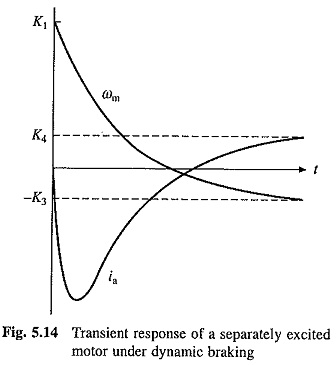
Transient Analysis of Dynamic Braking of Separately Excited Motor:

It is assumed that a constant active load torque T_L is acting on the motor shaft. Transient speed and current equations can be obtained by substituting new value for armature circuit resistance and V = 0 in Eqs. (5.30) and (5.31). This gives

Here also — K₃ and K₄ represent the steady state values of speed and current, respectively. This steady state running will occur when active load torque T_L is allowed to drive the motor in reverse direction. Initial conditions needed for the solution of these equations are obtained as:

It is assumed that at the initiation of braking the motor was running in steady state with load torque T_L. Then from Eq. (5.30)

For a general case K₁ is to be taken as the initial speed.

Braking can be applied with or without opening the armature circuit. When it is not opened, during transition from motoring to braking, the armature current continuity will be maintained and then initial value of current, from Eq. (5.31), will be K₂. However, if it is opened then the initial value of current will be zero. Here it is assumed that it is opened during transition. Therefore

Now from Eqs. (5.19) and (5.20), by substituting v = 0, i_a = 0 and ω_m = K₁.

Solutions of Eqs. (5.43) and (5.44) with the initial conditions of (5.46) to (5.49) will have the form:

where α₁ and α₂ are given by Eq. (5.38).

The nature of transient response under dynamic braking for the case of real α₁ and α₂ is shown in Fig. 5.14.

The transient equations for the plugging operation are obtained from (5.19), (5.20), (5.22) and (5.24) by substituting – v for v.

Energy Losses During Transient Operations:

Energy losses in motor and in resistors in motor armature circuit, if there are any, during transient period of operation, are required for selecting suitable ratings of motor and resistors. They are also needed to calculate the efficiency and effectiveness of the transient process.

Multiplying both sides of Eq. (5.16) by i_a gives

Considering the viscous friction torque to be a part of the load torque T_L, we have from Eq. (5.17)

Substituting from Eqs. (5.18) and (5.53) into (5.52) and integrating both sides of the resulting equation against time yield

This equation states that out of the total energy supplied by the source during a transient process, one portion is wasted in armature circuit resistance, second portion is stored in armature circuit inductance, third portion is stored in inertia of mechanical parts and the rest is consumed by the load. Energy stored in the armature circuit inductance is usually small compared to other energy terms, and therefore, will be neglected in subsequent analysis.

Starting of the motor with a constant applied voltage V and a load torque T_L is considered now.

Since

where ω_m0 is the ideal no load speed. From Eqs. (5.54) and (5.55)

Equation (5.56) gives an expression for energy loss in the armature circuit resistance of the machine. When started on no load the final (steady state) speed will be ω_m0. Hence, energy loss under no load condition E₀ is

It is interesting to note that the energy loss in motor armature circuit during starting without load is equal to the kinetic energy stored in rotating parts of the motor at steady state speed. Further, it is independent of the duration of starting process, nature of speed-torque and speed-current characteristics of the motor, number of steps in starting resistance and the value of reistance in each step.

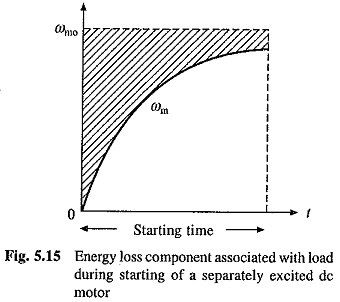
Since ω_m0 will not be very much different from the steady state speed with load T_L on the motor shaft, first term on R.H.S. of Eq. (5.56) approximately represents the copper loss during starting under no load and what has been said about E₀ is also applicable to this term. Second term depends on load-torque, motor speed-torque characteristics and the value of starting resistance. This term is represented by the shaded area of Fig. 5.15.

As stated above first term on right side of (5.56) remains unchanged with the change of starting resistance. It can however be lowered by reduced voltage method of starting. Let us consider the case in which source voltage is applied in a number of equal steps. First part of the copper loss on mth step will be

Since this part of the copper loss will be the same on all the n steps, total no load copper loss during starting becomes

Comparison of this with Eq. (5.57) shows that the no load copper loss has been reduced by a factor of n.

Let us next examine the loss during rheostatic braking. Substituting V = 0, neglecting L_a and assuming load torque to be constant and equal to T_L, the following equation can be derived from (5.52) and (5.53)

It has been assumed that prior to braking, motor was operating in steady state against a passive load torque T_L at a speed ω_mL. On integration Eq. (5.60) yields

This equation indicates that the load absorbs a part of stored kinetic energy and the rest is dissipated as copper loss.

For plugging, on substitution of —V for V and L_a = 0, in Eqs. (5.52) and (5.53) the following equation is obtained for the copper loss

From Eqs. (5.61) and (5.62) the no load copper losses under dynamic braking and plugging will be 1/2 Jω²₀ and 3/2 Jω²₀ respectively. Thus, loss during plugging will be three times that during dynamic braking. Since during plugging energy obtained from the kinetic energy of rotating parts is only 1/2 Jω²_m0, remainder Jω²_m0 is drawn from the supply.

Transient Analysis of Separately Excited Motor with Field Control:

Let the armature voltage be maintained constant. Now

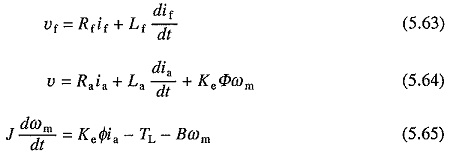
Here Φ is a nonlinear function of i_f. If saturation is neglected and Φ is assumed to be proportional to i_f then (5.64) and (5.65) can be written as

where K′ = K_eK_Φ.

Because of the terms K′i_fω_m and K′i_fi_a, which involve product of two variables, (5.66) and (5.67) are nonlinear equations, even though the saturation has been neglected. Thus, this analysis can be carried out using numerical methods of solving non-linear differential equations such as 4th order Runge-Kutta and Predictor-Corrector Methods.

A special case with the field control arises when the armature current is maintained constant. Then the dynamics of motor load system is described by Eq. (5.63) along with the following equation:

where K_a = K_eK_ΦI_a and I_a is the armature current.

From Eq. (5.68) expression of i_f and di_f/dt can be obtained. Substituting these in Eq. (5.63) and rearranging the’ terms gives

where

The motor can be analysed for its transient response using Eq. (5.69) provided the initial conditions are known. The initial value of ω_m will be known from the steady state operating point immediately before the transients and the initial value of dω_m/dt is calculated from Eq. (5.68).